home SITEMAP vers download page centrale PACK retour théorie
(GéKaDé EI)
 Un peu de théorie - suite
L'effet de peau (skin effect) est également appelé effet KELVIN
suite aux recherches de Lord Kelvin en 1887. Tesla à également fait des recherches dans ce domaine.
Pour des conducteurs en cuivre on calcule la résistance en µOhm/m : R=(261√f)/p [µΩ/m] où f est la fréquence et p le périmètre du conducteur en mm.
Cette formule détermine le diamètre pour lequel la ratio (résistance dc/impédance ac+dc) est environ 0,9, soit une augmentation de 10% des pertes par effet de peau.
Donc si on ajoute environ 10% de brins supplémentaires, on compense les pertes par effet de peau à la fréquence trouvée.

Pour un conducteur cylindrique en cuivre, on a les valeurs "d'épaisseur de peau" δ ci-dessous à gauche suivant la fréquence.
relation fréquence / épaisseur de peau

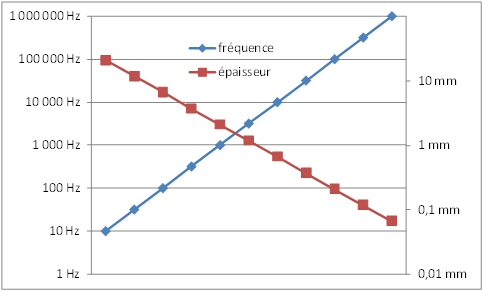
(Fréquences sinusoïdales, il faut corriger pour d'autres formes de signaux)

fréquence δ mm Øbrin mm courant par brin à
  optimum normalisé 4A/mm² 10A/mm²
4,4kHz 1,00 2,00 12,57A 31,43A
18kHz 0,495 1,00 3,14A 7,85A
27,5kHz 0,40 0,80 2,01A 5,03A
44,4kHz 0,315 0,63 1,25A 3,12A
70,5kHz 0,250 0,50 0,79A 1,96A
110kHz 0,200 0,40 0,50A 1,26A
140kHz 0,177 0,355 0,40A 0,99A
200kHz 0,148 0,3 282mA 0,71A
280kHz 0,125 0,25 196mA 491mA
440kHz 0,100 0,20 126mA 314mA
800kHz 0,074 0,15 71mA 177mA
1,15MHz 62µm 0,125 49mA 123mA
1,8MHz 49µm 0,10 31mA 79mA
2,75MHz 40µm 0,08 20mA 50mA
4,4MHz 32µm 0,063 12mA 31mA
7MHz 25µm 0,05 8mA 20mA
11MHz 20µm 0,04 5mA 13mA
17MHz 16µm 0,032 3,2mA 8mA
20MHz 15µm 0,03 2,8mA 7mA
35MHz 11,2µm 0,022 1,5mA 3,8mA
45MHz 9,9µm 0,02 1,26mA 3,14mA
70MHz 7,9µm 0,016 0,8mA 2mA































Ainsi pour 800kHz, le brin unitaire peut aller jusqu'au diamètre standard 0,15 et pour une densité de courant de 4A/mm² peut débiter 71mA par brin non ventilé.
Dans un transformateur d'alimentation à découpage à 35kHz non ventilé, on aura le un optimum pour un enroulement à 50A avec 32 brins de 0,71.
Dans un transformateur à 1MHz pour un enroulement de 25A il faut 475 brins de Ø0,125.

A noter qu'un optimum électrique pour l'effet de peau ne correspond pas nécessairement avec les autres contraintes (effet de proximité, pertes Joule, encombrement, facilité de bobinage, impératifs économiques) et qu'il faut trouver le juste équilibre!
Ainsi, bien qu'il soit techniquement possible de fabriquer des câbles de litz avec des brins de 0,8µm pour de très hautes fréquences,
on réalise des bobines pour la plage jusque 10GHz avec des brins unitaires de Ø0,02mm (20µm) en compensant l'effet de peau par une augmentation du nombre de brins.
En-dessous de 0,02mm le ratio cuivre/émail devient trop faible ce qui rend la fabrication et la manipulation de plus en plus délicate et cause d'énormes problèmes d'interconnexion pour des câbles complexes.
A noter qu'un petit brin de cuivre de Ø0,02mm aura du mal à supporter une traction de seulement 7cN!

Ci-après quelques explications disponibles sur internet:

(Voyez http://fr.wikipedia.org/wiki/Effet_de_peau)
L'épaisseur de peau détermine la largeur de la zone où se concentre le courant dans un conducteur. Elle permet de calculer la résistance effective à une fréquence donnée.
\delta = \sqrt{\frac {2} {\omega\cdot\mu\cdot\sigma}}\ = \sqrt{\frac {2\cdot\rho} {\omega\cdot\mu}}
\delta \, : épaisseur de peau en mètre [m]
\omega \, : pulsation en radian par seconde [rad/s] (\omega = 2\cdot\pi\cdot f)
f \, : fréquence du courant en Hertz [Hz]
\mu \, : perméabilité magnétique en Henry par mètre [H/m]
\rho \, : résistivité en ohm mètre [Ωm] (\rho = \frac 1 \sigma)
\sigma \, : conductivité électrique en Siemens par mètre [S/m]

Pour un conducteur de section significativement plus grande que δ, on peut calculer la résistance effective à une fréquence donnée en considérant que seule la partie extérieure d'épaisseur δ contribue à la conduction. Par exemple pour un conducteur cylindrique de rayon R on aura une section utile de :S_u = \pi\cdot{(R^2 - (R-\delta)^2)}

(Voyez https://f5zv.pagesperso-orange.fr/RADIO/RM/RM.html):
L'effet de peau ou effet pelliculaire 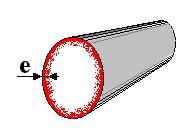(skin effect)

Les courants à haute fréquence ne se propagent pas dans les conducteurs comme le courant continu ou à basse fréquence. Au lieu d'utiliser la totalité de la section du conducteur ils se cantonnent dans les couches proches de la surface du conducteur. La densité de courant décroît de façon exponentielle au fur et à mesure que l'on s'éloigne de la surface. L'épaisseur moyenne e (en m) de la "peau" dans laquelle circule les courants HF peut être estimée à l'aide de la formule:

µo : perméabilité magnétique du vide (4p.10-7)
µr : perméabilité magnétique relative du conducteur (on prendra 1 pour le cuivre)
f : fréquence en Hz
r : résistivité du conducteur en W.m (18.10-9 W.m pour le cuivre)
La résistance d'un conducteur en HF est plus importante qu'en continu.

... pour que le courant passe ...